[알고리즘] 그래프_플로이드 워셜 알고리즘
플로이드-워셜 알고리즘은 그래프 자료구조에서 사용하는 경로 탐색 알고리즘입니다. 시간 복잡도가 \(O(v^3)\)으로
꽤 느리지만, 그래프에서 모든 경로의 최단 거리를 구하기 위해서 사용할 수 있는 유용한 알고리즘입니다.
이 알고리즘은 로버트 W. 플로이드(1936)과 스테판 워셜(1935)의 이름을 따서 명명되었으며, 더욱 이전에 플로이드-워셜 알고리즘과 근본적으로 같은 내용의 알고리즘을 제안한 버나드 로이(1934)의 이름을 따서 로이-워셜, 로이-플로이드 알고리즘이라고도 부릅니다.
시간복잡도 \(O(v^3)\)
플로이드-워셜 알고리즘의 핵심은 중간 경로입니다. \(v_1\)에서 \(v_2\)로 가는 사이에 중간경로 \(v_m\)을 두었을 때, 완성되는 경로가 연결될 때, 그 경로의 거리가 현재까지 최단이면 저장하는 방식입니다.

그래프를 인접리스트로 나타내면 위와 같습니다. INF는 경로가 없는 두 정점 사이의 거리를 무한대(infinite)로 표시한 것입니다. 이 인접리스트로부터 플로이드-워셜 알고리즘을 적용하고, 모든 경로 사이의 최단 거리를 구해보겠습니다. 먼저 거리 배열을 Graph 배열과 같은 값으로 초기화합니다. (만약, Graph 배열의 간선 사이 정보를 더 이상 활용하지 않고 최단 거리를 구하는 것이 목적이라면 Graph 배열을 사용하여도 됩니다)
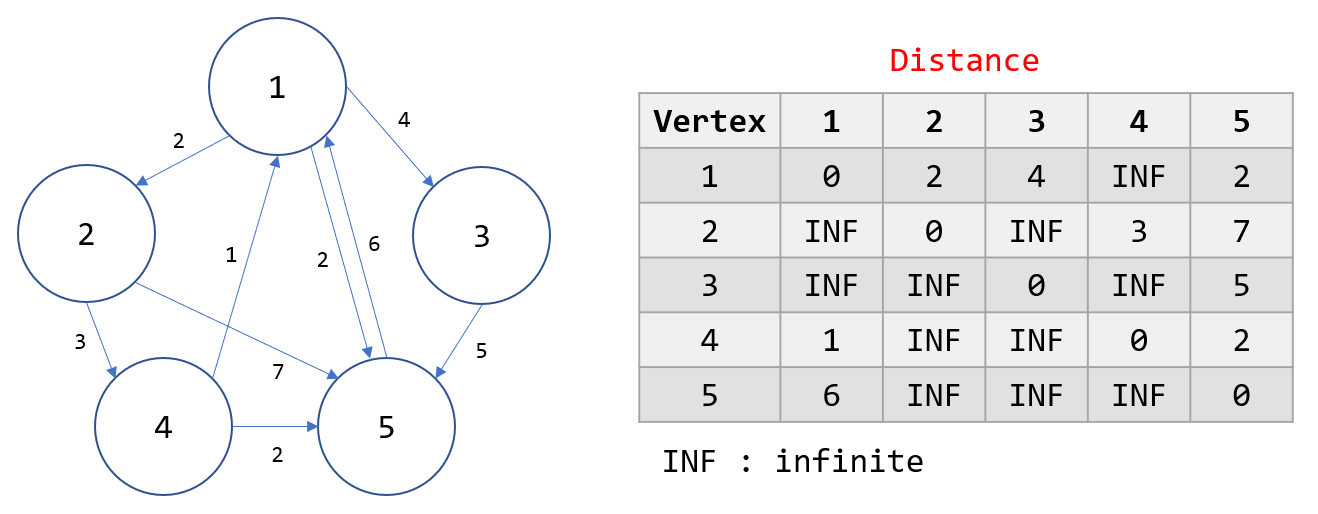
Distance 인접리스트를 만들었습니다. 그리고 플로이드-워셜 알고리즘을 적용하기 위해 모든 경로에 중간 경로를 추가했을 때의 최단 거리를 구합니다. 예를 들어, 중간 경로를 1로 정한다면, 모든 노드(2,3,4,5)에서 다른 노드(2,3,4,5)로 가는 경로에 2 노드를 거쳐가는 경로를 확인하고, 최단거리가 존재한다면 이를 저장합니다.

1을 중간 경로로 정하면 위와 같이 구할 수 있습니다. 4에서 1을 거쳐 갈 수 있는 경로들이 있고, 5에서 1을 거쳐 갈 수 있는 경로들이 있는데, 이 경로들이 지정된 경로보다 짧다면 distance 인접리스트를 갱신합니다.
위에서 하나의 예를 들어 설명하자면, (4→1→2)로 가는 경로는 3의 비용이 소모되며 원래의 경로 INF(무한대)보다 작으므로 4→2의 경로를 3으로 갱신합니다.

1을 중간 경로로 정하여 구한 인접리스트에 2를 중간 경로로 정하여 갱신하면 위와 같이 구할 수 있습니다. 2를 거쳐 갈 수 있는 경로에는 1에서 2를 거쳐갈 수 있는 경로들이 포함됩니다.
1을 중간 경로로 설정했을 때처럼 (1→2→4)의 경로 5(1→...→4)가 구해집니다.
그리고 (5→...→4)의 경로가 11로 갱신된 것을 확인할 수 있습니다. 이 결과는 이전에 1을 중간 경로로 설정했을 때, (5→1→2)의 경로를 찾았고, (2→4)의 경로를 활용하여, 2를 중간 경로로 하여 (5→1→2→4)의 경로를 완성한 것입니다. 이렇게 이전에 중간 경로로 정했던 다른 경로들은 다음의 작업에서도 영향을 미치며, 이런 결과로 플로이드-워셜 알고리즘이 최적해를 찾을 수 있음을 보장할 수 있습니다.
#include<iostream>
#include<string>
#include<vector>
using namespace std;
const int INF = 9'999'999;
int n;
int map[101][101];
void init() {
// 인접리스트를 만듭니다. n은 사이즈이고, 모든 경로를 입력받습니다.
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> map[i][j];
if (i != j && map[i][j] == 0) map[i][j] = INF;
}
}
}
void solution() {
// 실제 플로이드-워셜 알고리즘의 핵심입니다.
// k가 중간 경로이고, i와 j는 i에서 j로 향할 때 중간 경로를 k로 설정함을 의미합니다.
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
map[i][j] = min(map[i][j], map[i][k] + map[k][j]);
}
}
}
// 결과를 출력합니다.
cout << '\n';
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (map[i][j] >= INF) cout << "INF ";
else cout << map[i][j] << ' ';
}
cout << '\n';
}
}
int main() {
init();
solution();
}